Examlex

Solved

Suppose There Exists , So That for Any

question 25

Multiple Choice

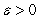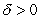Suppose there exists Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. , so that for any Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. we can find Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. 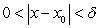satisfying Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. and Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. . We may conclude that:

Definitions:

Related Questions

Q2: Which of the following is/are not correct

Q7: We can use the difference quotient <img

Q12: A company that manufactures health food snacks

Q16: To compute the volume of the solid

Q17: Based on the expected value approach, the

Q18: Management styles differ among organizations and may

Q26: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate ."

Q31: Compute the standard deviation for each action.

Q50: The volume of a sphere of radius

Q63: Compute the following limits:<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute