Examlex

Solved

If and Then Does Not Converge to a Finite

question 76

Multiple Choice

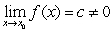If If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 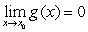and If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 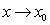then If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 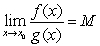does not converge to a finite limit as If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
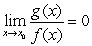For proving, we assume that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. exists and is finite. Then
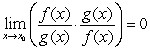By the Quotient Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. and by the Product Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
Which of the statements below completes the proof?

Definitions:

Episodic Memory

A type of long-term memory that involves the recollection of specific events, situations, and experiences.

Gene

DNA segment that encodes the synthesis of a particular protein.

Gene Expression

The process by which information from a gene is used in the synthesis of a functional gene product, often proteins.

Identical Twins

Identical twins are siblings born from the same fertilized egg, resulting in them sharing identical genetic material.

Related Questions

Q13: The vertical tank shown in the figure

Q17: Which of the following measures is used

Q17: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be

Q24: After transforming data, a model of retail

Q32: Write the null and alternative hypothesis.

Q59: What is an equation of the tangent

Q64: Sketch the graph of the function. Indicate

Q70: Find the volume of the solid shown

Q72: At the 0.05 level of significance, the

Q74: The domain and range of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"