A Second Order Differential Equation Can Be Arranged to the Form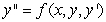

question 25

Multiple Choice

A second order differential equation can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 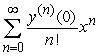, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x⁴ in the Taylor polynomial expansion of the solution to the equation 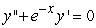if the initial conditions are ?

---

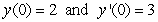Definitions:

Global Team

A group of individuals working together from various geographical locations, leveraging digital tools to achieve common goals.

Native Language

The first language a person learns to speak in childhood, which is often the primary means of communication in their daily life.

Global Team

A group of individuals working across time zones, borders, and cultures towards a common business goal or project, often facilitated by technology.

Member Tolerance

refers to the ability of individuals within a group or team to accommodate and adapt to differences among members, such as divergent opinions, behaviors, or working styles.