Examlex

Solved

A Second Order Differential Equaiton Can Be Arranged to the Form

question 17

Multiple Choice

A second order differential equaiton can be arranged to the form A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) , and one can find the third and higher derivatives of y by simply differentiating this equation. 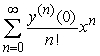Since a Taylor series expansion of a function y(x) is A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . 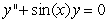What does the fourth-degree Taylor polynomial look like for the solution to the equation A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? 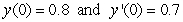A) B) C) D) if the initial conditions are A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) ?

Definitions:

Managed Care

A healthcare delivery system aimed at managing cost, quality, and utilization of services to provide cost-effective care.

Assertive Community Treatment

is an intensive, team-based approach to mental health care, focusing on providing comprehensive services to individuals with serious mental illnesses in their communities.

Psychiatric Status

The current state or condition of an individual's mental health, as assessed by a mental health professional.

Housing Adequacy

The suitability of living conditions in terms of safety, space, and basic amenities, contributing to overall well-being.

Related Questions

Q27: Given <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Given ,

Q62: Identify the region (solid lines) and axis

Q68: Use the contour plot to estimate <img

Q69: Use a CAS to estimate the arc

Q74: Find symmetric equations of the line through

Q77: Set up and evaluate the integral <img

Q77: Use Riemann sums and a limit to

Q101: Calculate the first two steps of the

Q103: A projectile is fired with initial speed

Q104: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find