A Second Order Differential Equation Can Be Arranged to the Form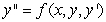

question 25

Multiple Choice

A second order differential equation can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 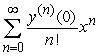, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x⁴ in the Taylor polynomial expansion of the solution to the equation 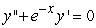if the initial conditions are ?

---

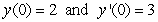Definitions:

Standard Cost System

An accounting method that uses cost standards for material, labor, and overhead charges to control costs and assess operational efficiency.

Direct Labor Standards

Direct Labor Standards define the expected labor time and cost necessary to produce a unit of product, facilitating budgeting and performance evaluation.

Work in Process

Inventory category that includes items currently being manufactured but not yet completed.

Standard Cost System

A standard cost system is an accounting method that uses cost estimates to predict the cost of production under normal conditions.