A Second Order Differential Equaiton Can Be Arranged to the Form

question 17

Multiple Choice

A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 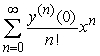, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation 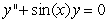if the initial conditions are ?

---

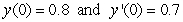Definitions:

Investigative Authority

The legal power or mandate given to an individual or organization to conduct investigations, often related to law enforcement or regulatory compliance.

Enabling Statutes

Enabling statutes are laws passed by a legislative body that grant certain powers or authority to a government agency or an official to implement or enforce other laws.

Administrative Regulatory Agency

A governmental body responsible for exercising autonomous authority over some area of human activity in a regulatory or supervisory capacity.

Freedom of Information Act Exemptions

are specific categories of information exempted from disclosure under the Freedom of Information Act, including matters of national security, personal privacy, and law enforcement.