A Phase Portrait of a Predator-Prey System Is Given Below

question 120

Essay

A phase portrait of a predator-prey system is given below in which F represents the population of foxes (in thousands) and R the population of rabbits (in thousands). 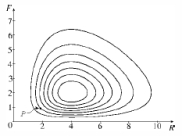(a) Referring to the graph, what is a reasonable non-zero equilibrium solution for the system?
(b) Write down a possible system of differential equations which could have been used to produce the given graph.(c) Describe how each population changes as time passes, using the initial condition P indicated on the graph.(d) Use your description in part (c) to make a rough sketch of the graph of R and F as functions of time.

---

Definitions:

Market Growth Rate

The increase in size or value of a market over a specified period, typically expressed as a percentage.

Demand Curve

A graphical representation showing the relationship between the price of a product and the quantity of the product that consumers are willing to purchase.

Parabola

A symmetrical, open plane curve formed by the intersection of a cone with a plane parallel to its side.

Diagonal Line

A line segment that joins two non-adjacent vertices in a polygon or two vertices in a polyhedron that are not on the same face, often creating a sense of movement in artwork or design.