The Orbits of the Planets Can Be Modeled Easily by Assuming

question 33

Essay

The orbits of the planets can be modeled easily by assuming i). that the sun is a perfect sphere and ii). that each planet is influenced only by the gravitational field of the sun (that is, each planet is unperturbed by gravitational forces from other planets, distant stars, etc.). According to Newton's (classical) theory of gravity, these assumptions result in elliptical planetary orbits with the sun at one focus. That is, the orbit can be described by the polar equation . However, according to Einstein's (relativistic) theory of gravitation, the orbits are more accurately described by 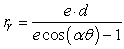, where is a constant such that 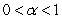. Describe how the inclusion of the factor 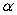affects the orbit. That is, compare the classical orbit to the relativistic orbit. How do they differ? Draw figures that summarize the differences in the classical and relativistic orbits.

Understand the concept of muscle groups working together for common actions.

Describe the anatomical features and definitions relevant to the lower limb.

Compare and contrast the muscle architectures and movement capabilities of the lower limb to other parts of the body.

Understand basic concepts of correlation and how it is calculated.

---

Definitions:

Secondary Growth

Growth produced by lateral meristems, thickening the roots and shoots of woody plants.

Vascular Cambium

The vascular cambium is a layer of dividing cells in plants, responsible for producing new phloem and xylem, contributing to the plant's secondary growth.

Bark

The outer protective layer of a tree's trunk, branches, and roots, comprised of dead cells.

Organelles

Specialized structures within a cell that perform specific functions necessary for the cell's life, such as mitochondria, chloroplasts, and the Golgi apparatus.