A Second Order Differential Equation Can Be Arranged to the Form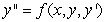

question 19

Multiple Choice

A second order differential equation can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 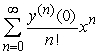, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x⁴ in the Taylor polynomial expansion of the solution to the equation if the initial conditions are ?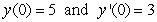

---

Definitions:

Synergy

The interaction or cooperation of two or more organizations, substances, or other agents to produce a combined effect greater than the sum of their separate effects.

Life Cycle Stages

The various phases through which an entity, such as a product, organization, or project, passes, typically including initiation, growth, maturity, and decline.

Formal Work Unit

A structured group within an organization designed to perform specific tasks or functions according to defined roles and procedures.

Temporary Task Force

A short-term group set up to achieve a specific objective or to solve a specific problem within an organization.