A Second Order Differential Equaiton Can Be Arranged to the Form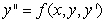

question 2

Multiple Choice

A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 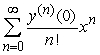, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation 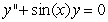if the initial conditions are ?

---

Definitions:

Residual Income

The income that remains after subtracting all required costs of capital from operating income, a measure of profitability.

Minimum Required Rate

The lowest rate of return that an investment must yield to be considered acceptable, often tied to the cost of capital or inflation.

Investment Opportunity

A financial investment or asset that has the potential to yield returns or profits.

Residual Income

The income that remains after deducting all required costs of capital from the operating income, used as a performance measure.