A Second Order Differential Equaiton Can Be Arranged to the Form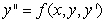

question 2

Multiple Choice

A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 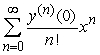, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation 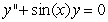if the initial conditions are ?

---

Definitions:

\(k ^ { 3 }\)

Represents the cube of a variable \(k\), equivalent to multiplying \(k\) by itself twice (\(k*k*k\)).

\(k + 8\)

An algebraic expression representing the sum of a variable, \(k\), and the number 8.

\(d = \frac { 3 } { 7 }\)

Represents a specific value of the variable d, which is equal to the fraction three-sevenths.