(A)Estimate a Simple Linear Regression Model Involving Shipping Cost and Package

question 53

Essay

(A)Estimate a simple linear regression model involving shipping cost and package weight.Interpret the slope coefficient of the least squares line as well as the computed value of .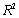
(B)Add another explanatory variable - distance shipped - to the regression to (A).Estimate and interpret this expanded model.How does the 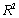value for this multiple regression model compare to that of the simple regression model estimated in (A)? Explain any difference between the two values.Compute and interpret the adjusted 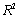value for the revised model.
(C)Suppose that one of the managers of this express delivery service company is trying to decide whether to add an interaction term involving the package weight 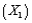and the distance shipped 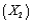in the multiple regression model developed previously.Why would the manager want to add such a term to the regression equation?
(D)Estimate the revised model using the interaction term suggested in (C).
(E)Interpret each of the estimated coefficients in your revised model in (D).In particular,how do you interpret the coefficient for the interaction term in the revised model?
(F)Does this revised model in (D)fit the given data better than the original multiple regression model in (B)? Explain why or why not.

---

Definitions:

Role Expectations

The anticipated behaviors and actions associated with a particular social status or position within a group or society.

Conflict Theory

A sociological perspective that focuses on the tensions and conflicts in society, emphasizing the competition for limited resources and the struggles between different social classes or groups.

Social Inequality

The existence of unequal opportunities and rewards for different social positions or statuses within a group or society.

Conflict Theory

A sociological perspective that sees social life as a competition, focusing on the struggle for resources, power, and inequality.