The Introductory Biology Class at State University Is Conducting a Study

question 21

Multiple Choice

The introductory biology class at State University is conducting a study of water quality in their local community.The population mean of a certain beneficial bacteria found in drinking water ( 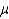) is 100,with 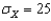.The bacteria counts from the community are given below.Use a two-tailed rejection region with a total area of 0.05.What should you conclude?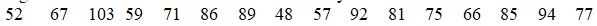

• A)Since the z-value falls within the region of rejection,we should conclude this sample mean likely represents some other population.
• B)Since the z-value does not fall within the region of rejection,we should not conclude this sample mean represents some other population.
• C)Since the z-value falls within the region of rejection,we should not conclude this sample mean represents some other population.
• D)Since the z-value does not fall within the region of rejection,we should conclude this sample mean likely represents some other population.

---

Definitions:

Standard Deviation

A measure of the dispersion or variability of a set of values, indicating how much the values differ from the mean of the set.

Boys And Girls

Refers to male and female children or adolescents collectively.

Standard Deviation

A measure of the amount of variation or dispersion from the average in a set of data points, representing how spread out the values are.

Larger Contract

A contract or agreement that is significant in terms of its scope, value, or both.