To Examine the Differences Between Salaries of Male and Female

question 91

Multiple Choice

To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses) ,
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β₀ + β₁ Educ + β₂ Exper + β₃ Train + β₄ Gender + ε Model B: Salary = β₀ + β₁ Educ + β₂ Exper + β₃ Gender + ε 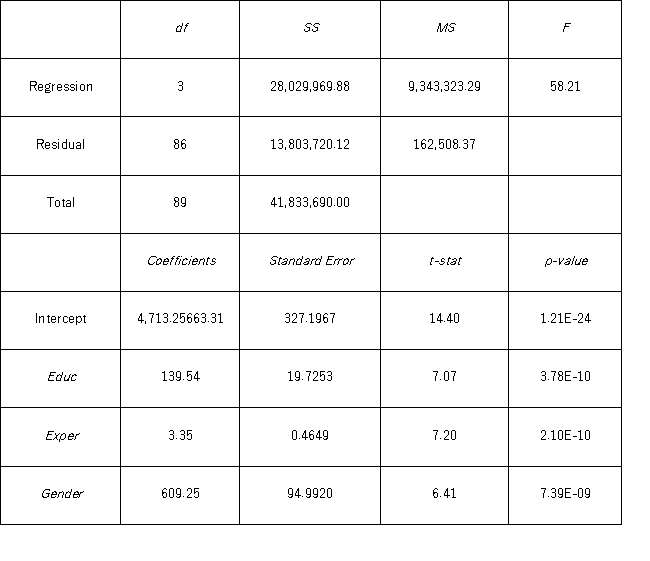A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the conclusion of the appropriate test at 10% significance level?

• A) Do not reject H₀;the salaries of female managers cannot be proven to be lower on average by more than $500.
• B) Reject H₀;the salaries of female managers cannot be proven to be lower on average by more than $500.
• C) Do not reject H₀;the salaries of female managers are lower on average by more than $500.
• D) Reject H₀;the salaries of female managers are lower on average by more than $500.