It is believed that the sales volume of one-liter Pepsi bottles depends on the price of the bottle and the price of a one-liter bottle of Coca-Cola.The following data have been collected for a certain sales region.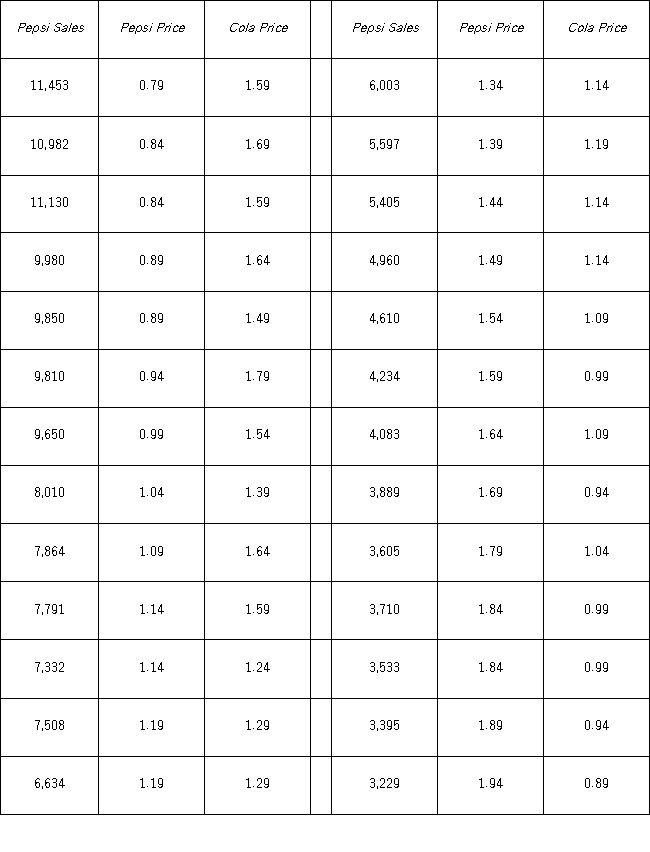 
Using Excel's regression,the linear model Pepsi Sales = β0 + β1Pepsi Price + β2Cola Price + ε and the log-log model ln(Pepsi Sales)= β0 + β1ln(Pepsi Price)+ β2ln(Cola Price)+ ε have been estimated as follows: 
What is the percentage of variations in ln(PepsiSales)as explained by the estimated log-log model?
Definitions:
Type II Error
The error that occurs when the null hypothesis is not rejected when it is actually false, also known as a "false negative".
Sample Size
The number of observations or units chosen from a population for the purpose of statistical analysis.
Lowering Alpha
Reducing the alpha level, or the threshold of significance, to decrease the probability of committing a type I error in hypothesis testing.
Type I Error
A statistical error occurring when a true null hypothesis is incorrectly rejected.
Q2: Becky owns a diner and is concerned
Q5: Consider the following regression model: Humidity =
Q28: Almas Mohammed paid $50 for a stock
Q40: The following table shows the distribution of
Q58: The following data for five years of
Q58: A seasonal component differs from a cyclical
Q71: Conditional on x<sub>1</sub>,x<sub>2</sub>,... ,x<sub>k</sub>,the error term ε
Q81: When two regression models applied on the
Q107: A card-dealing machine deals spades (1),hearts (2),clubs
Q116: Refer to the portion of regression results