Your Textbook Used the California Standardized Testing and Reporting (STAR)data

question 43

Essay

Your textbook used the California Standardized Testing and Reporting (STAR)data set on test student performance in Chapters 4-7.One justification for putting second to twelfth graders through such an exercise once a year is to make schools more accountable.The hope is that schools with low scores will improve the following year and in the future.To test for the presence of such an effect,you collect data from 1,000 L.A.County schools for grade 4 scores in 1998 and 1999,both for reading (Read)and mathematics (Maths).Both are on a scale from zero to one hundred.The regression results are as follows (homoskedasticity-only standard errors in parentheses): 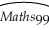= 6.967 + 0.919 ,R2 = 0.825,SER = 7.818
(0.542)(0.013) = 4.131 + 0.943, = R2 = 0.887,SER = 6.416
(0.409)(0.011)
(a)Interpret the results and indicate whether or not the coefficients are significantly different from zero.Do the coefficients have the expected sign and magnitude?
(b)Discuss various threats to internal and external validity,and try to assess whether or not these are likely to be present in your study.
(c)Changing the estimation method to allow for heteroskedasticity-robust standard errors produces four new standard errors: (0.539), (0.015), (0.452),and (0.015)in the order of appearance in the two equations above.Given these numbers,do any of your statements in (b)change? Do you think that the coefficients themselves changed?
(d)If reading and maths scores were the same in 1999 as in 1998,on average,what coefficients would you expect for the intercept and the slope? How would you test for the restrictions?
(e)The appropriate F-statistic in (d)is 138.27 for the maths scores,and 104.85 for the reading scores.Comparing these values to the critical values in the F table,can you reject the null hypothesis in each case?
(f)Your professor tells you that the analysis reminds her of "Galton's Fallacy." Sir Francis Galton regressed the height of children on the average height of their parents.He found a positive intercept and a slope between zero and one.Being concerned about the height of the English aristocracy,he interpreted the results as "regression to mediocrity" (hence the name regression).Do you see the parallel?

---

Definitions:

Nature

The phenomena of the physical world collectively, including plants, animals, the landscape, and other features and products of the earth, as opposed to humans or human creations.

Submarine

A watercraft capable of independent operation underwater, often used for naval or research purposes.

Hydrosphere

All the waters on the earth's surface, such as lakes and seas, and sometimes including water over the earth's surface, such as clouds.

Exploration Tool

Equipment or software used in the discovery and investigation of new geographical areas or resources.