Macroeconomists Who Study the Determinants of Per Capita Income (The

question 8

Essay

Macroeconomists who study the determinants of per capita income (the "wealth of nations")have been particularly interested in finding evidence on conditional convergence in the countries of the world.Finding such a result would imply that all countries would end up with the same per capita income once other variables such as saving and population growth rates,education,government policies,etc. ,took on the same value.Unconditional convergence,on the other hand,does not control for these additional variables.
(a)The results of the regression for 104 countries was as follows, 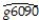= 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
(0.004)(0.0073),
where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.
For the 24 OECD countries in the sample,the output is = 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
(0.004)(0.0063)
Interpret the results and point out the difference with regard to unconditional convergence.
(b)The "beta-convergence" regressions in (a)are of the following type, 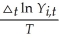= β0 + β0 ln Yi,0 + ui,t,
where △t ln Yi,t = ln Yi,0 - ln Yi,0,and t and o refer to two time periods,i is the i-th country.
Explain why a significantly negative slope implies convergence (hence the name).
(c)The equation in (b)can be rewritten without any change in information as (ignoring the division by T)
ln Yt = β0 + γ1 ln Y0 + ut
In this form,how would you test for unconditional convergence? What would be the implication for convergence if the slope coefficient were one?
(d)Let's write the equation in (c)as follows: 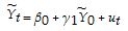and assume that the "~" variables contain measurement errors of the following type, 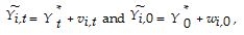where the "*" variables represent true,or permanent,per capita income components,while v and w are temporary or transitory components.Subtraction of the initial period from the current period then results in 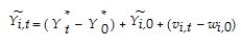Ignoring,without loss of generality,the constant in the above equation,and making standard assumptions about the error term,one can show that by regressing current per capita income on a constant and the initial period per capita income,the slope behaves as follows: 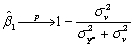Discuss the implications for the convergence results above.

Comprehend the impact of noise on the effectiveness of marketing communication.

Understand the concept of encoding and decoding in the communication process.

Recognize the importance of a mutual field of experience for effective communication.

Identify potential errors in communication and strategies to mitigate them.

---

Definitions:

UV Light

Ultraviolet light, a type of electromagnetic radiation with a wavelength shorter than that of visible light but longer than X-rays, affecting living tissues.

Radiographically Labeled

Marked or tagged with a radiographic marker for visualization under X-rays or similar imaging techniques.

Blotting Buffer

A solution used in molecular biology techniques to transfer proteins, DNA, or RNA onto a membrane for detection and analysis.

UV Light

Ultraviolet light, a type of electromagnetic radiation which is not visible to the human eye and has shorter wavelengths than visible light but longer than X-rays.