One of the Most Frequently Estimated Equations in the Macroeconomics

question 10

Essay

One of the most frequently estimated equations in the macroeconomics growth literature are so-called convergence regressions.In essence the average per capita income growth rate is regressed on the beginning-of-period per capita income level to see if countries that were further behind initially,grew faster.Some macroeconomic models make this prediction,once other variables are controlled for.To investigate this matter,you collect data from 104 countries for the sample period 1960-1990 and estimate the following relationship (numbers in parentheses are for heteroskedasticity-robust standard errors): 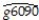= 0.020 - 0.360 × gpop + 0.00 4 × Educ - 0.053×RelProd60,R2=0.332,SER = 0.013
(0.009)(0.241)(0.001)(0.009)
where g6090 is the growth rate of GDP per worker for the 1960-1990 sample period,RelProd60 is the initial starting level of GDP per worker relative to the United States in 1960,gpop is the average population growth rate of the country,and Educ is educational attainment in years for 1985.
(a)What is the effect of an increase of 5 years in educational attainment? What would happen if a country could implement policies to cut population growth by one percent? Are all coefficients significant at the 5% level? If one of the coefficients is not significant,should you automatically eliminate its variable from the list of explanatory variables?
(b)The coefficient on the initial condition has to be significantly negative to suggest conditional convergence.Furthermore,the larger this coefficient,in absolute terms,the faster the convergence will take place.It has been suggested to you to interact education with the initial condition to test for additional effects of education on growth.To test for this possibility,you estimate the following regression: 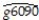= 0.015 - 0.323 × gpop + 0.005 × Educ - 0.051 × RelProd60
(0.009)(0.238)(0.001)(0.013)
-0.0028 × (EducRelProd60),R2=0.346,SER = 0.013
(0.0015)
Write down the effect of an additional year of education on growth.West Germany has a value for RelProd60 of 0.57,while Brazil's value is 0.23.What is the predicted growth rate effect of adding one year of education in both countries? Does this predicted growth rate make sense?
(c)What is the implication for the speed of convergence? Is the interaction effect statistically significant?
(d)Convergence regressions are basically of the type
Δln Yt = β0 - β1 ln Y0
where △ might be the change over a longer time period,30 years,say,and the average growth rate is used on the left-hand side.You note that the equation can be rewritten as
△ln Yt = β0 - (1 - β1)ln Y0
Over a century ago,Sir Francis Galton first coined the term "regression" by analyzing the relationship between the height of children and the height of their parents.Estimating a function of the type above,he found a positive intercept and a slope between zero and one.He therefore concluded that heights would revert to the mean.Since ultimately this would imply the height of the population being the same,his result has become known as "Galton's Fallacy." Your estimate of β1 above is approximately 0.05.Do you see a parallel to Galton's Fallacy?

---

Definitions:

Binary Arithmetic

A fundamental area of computer science focusing on arithmetic operations, such as addition and multiplication, using binary numbers.

Unary Arithmetic

Operations in mathematics and computer science that operate on a single operand or value to produce a new value.

Cast Operator

In programming, a cast operator converts one data type into another, providing a way to override the automatic data type conversions.

Binary Operator

An operator that works on two operands and performs operations such as addition, subtraction, multiplication, etc.