In the case of perfect multicollinearity,OLS is unable to calculate the coefficients for the explanatory variables,because it is impossible to change one variable while holding all other variables constant.To see why this is the case,consider the coefficient for the first explanatory variable in the case of a multiple regression model with two explanatory variables: 
(small letters refer to deviations from means as in 
).
Divide each of the four terms by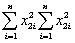 
to derive an expression in terms of regression coefficients from the simple (one explanatory variable)regression model.In case of perfect multicollinearity,what would be R2 from the regression of 
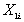on 
? As a result,what would be the value of the denominator in the above expression for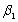 
?
Definitions:
Normal Functions
The regular operations or activities that are typical for a system, organ, or part, ensuring proper health and performance.
Hallucinations
False perceptions of objects, events, or sensations without any external stimulus, often occurring in mental disorders.
Voices
In psychology, often refers to auditory hallucinations that involve hearing voices without external stimuli, typically associated with conditions like schizophrenia.
Maladaptive
Anything that does not allow a person to function within or adapt to the stresses and everyday demands of life.
Q4: The distributed lag model relating orange juice
Q24: The extended least squares assumptions in the
Q26: When your multiple regression function includes a
Q30: (Requires Appendix material)If X and Y are
Q34: The administration of your university/college is thinking
Q38: Using the model Y = Xβ +
Q39: Finding a small value of the p-value
Q42: The following are properties of the logarithm
Q50: In the multiple regression model,the least squares
Q62: You have collected data from Major League