The Administration of Your University/college Is Thinking About Implementing a Policy

question 35

Essay

The administration of your university/college is thinking about implementing a policy of coed floors only in dormitories.Currently there are only single gender floors.One reason behind such a policy might be to generate an atmosphere of better "understanding" between the sexes.The Dean of Students (DoS)has decided to investigate if such a behavior results in more "togetherness" by attempting to find the determinants of the gender composition at the dinner table in your main dining hall,and in that of a neighboring university,which only allows for coed floors in their dorms.The survey includes 176 students,63 from your university/college,and 113 from a neighboring institution.
(a)The Dean's first problem is how to define gender composition.To begin with,the survey excludes single persons' tables,since the study is to focus on group behavior.The Dean also eliminates sports teams from the analysis,since a large number of single-gender students will sit at the same table.Finally,the Dean decides to only analyze tables with three or more students,since she worries about "couples" distorting the results.The Dean finally settles for the following specification of the dependent variable:
GenderComp= Where " 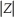" stands for absolute value of Z.The variable can take on values from zero to fifty.Briefly analyze some of the possible values.What are the implications for gender composition as more female students join a given number of males at the table? Why would you choose the absolute value here? Discuss some other possible specifications for the dependent variable.
(b)After considering various explanatory variables,the Dean settles for an initial list of eight,and estimates the following relationship: 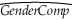= 30.90 - 3.78 × Size - 8.81 × DCoed + 2.28 × DFemme + 2.06 × DRoommate
- 0.17 × DAthlete + 1.49 × DCons - 0.81 SAT + 1.74 × SibOther, =0.24,SER = 15.50
where Size is the number of persons at the table minus 3,DCoed is a binary variable,which takes on the value of 1 if you live on a coed floor,DFemme is a binary variable,which is 1 for females and zero otherwise,DRoommate is a binary variable which equals 1 if the person at the table has a roommate and is zero otherwise,DAthlete is a binary variable which is 1 if the person at the table is a member of an athletic varsity team,DCons is a variable which measures the political tendency of the person at the table on a seven-point scale,ranging from 1 being "liberal" to 7 being "conservative," SAT is the SAT score of the person at the table measured on a seven-point scale,ranging from 1 for the category "900-1000" to 7 for the category "1510 and above," and increasing by one for 100 point increases,and SibOther is the number of siblings from the opposite gender in the family the person at the table grew up with.
Interpret the above equation carefully,justifying the inclusion of the explanatory variables along the way.Does it make sense to interpret the constant in the above regression?
(c)Had the Dean used the number of people sitting at the table instead of Number-3,what effect would that have had on the above specification?
(d)If you believe that going down the hallway and knocking on doors is one of the major determinants of who goes to eat with whom,then why would it not be a good idea to survey students at lunch tables?

---

Definitions:

DSM-5

A crucial reference for healthcare providers, the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition, provides comprehensive direction on diagnosing mental illnesses.

Bulimia Nervosa

An eating disorder marked by binge eating followed by methods to avoid weight gain, such as vomiting.

Anorexia Nervosa

An eating disorder characterized by an intense fear of gaining weight and a distorted body image, leading to severe restriction of food intake.

Purging Behavior

Actions such as vomiting or misuse of laxatives to rid the body of food and calories, commonly associated with eating disorders.