(Continuation from Chapter 4,number 6)The neoclassical growth model predicts that for identical savings rates and population growth rates,countries should converge to the per capita income level.This is referred to as the convergence hypothesis.One way to test for the presence of convergence is to compare the growth rates over time to the initial starting level.
(a)The results of the regression for 104 countries were as follows: 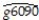 = 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
= 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
(0.004)(0.0073)  where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.Numbers in parenthesis are heteroskedasticity robust standard errors.
where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.Numbers in parenthesis are heteroskedasticity robust standard errors.
Using the OLS estimator with homoskedasticity-only standard errors,the results changed as follows: 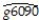 = 0.019 - 0.0006×RelProd60,R2= 0.00007,SER = 0.016
= 0.019 - 0.0006×RelProd60,R2= 0.00007,SER = 0.016
(0.002)(0.0068)
Why didn't the estimated coefficients change? Given that the standard error of the slope is now smaller,can you reject the null hypothesis of no beta convergence? Are the results in the second equation more reliable than the results in the first equation? Explain.
(b)You decide to restrict yourself to the 24 OECD countries in the sample.This changes your regression output as follows (numbers in parenthesis are heteroskedasticity robust standard errors):  = 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
= 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
(0.004)(0.0063)
Test for evidence of convergence now.If your conclusion is different than in (a),speculate why this is the case.
(c)The authors of your textbook have informed you that unless you have more than 100 observations,it may not be plausible to assume that the distribution of your OLS estimators is normal.What are the implications here for testing the significance of your theory?
Definitions:
Participants
Individuals or entities that take part in a study or research project.
T-test
A statistical procedure used to determine if there is a significant difference between the means of two groups under consideration, often used in small sample sizes.
Independent Means
A statistical method comparing the means of two independent groups to assess whether there is a significant difference.
Participants
Participants are individuals who take part in a research study, contributing data for analysis.
Q1: Some macroeconomic theories suggest that there is
Q9: Swaps obligate delivery of either bonds or
Q12: The conditional distribution of Y given X
Q13: You have collected quarterly data for the
Q14: Unit root tests<br>A)use the standard normal distribution
Q35: Show that for the following regression model<br>Yt
Q36: When the law of one price is
Q48: Your textbooks gives several examples of quasi
Q56: You have estimated the following regression to
Q62: Show that the correlation coefficient between Y