Let 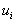Be Distributed N(0, ),I

question 53

Essay

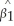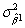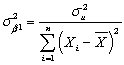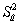Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect 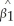to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about 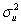can be incorporated about the tails of the t-distribution as the degrees of freedom increase.

---

Definitions:

Ignition Wires

Electrical cables in an internal combustion engine that deliver high voltage from the ignition coil to the spark plugs to ignite the fuel-air mixture.

Gas Tank

A container for storing fuel in a vehicle.

Emotional Intelligence

The aptitude for comprehending, overseeing, and expressing personal emotions, coupled with the capability to conduct oneself thoughtfully and empathically in dealings with others.

Academic Aptitude

The capability to succeed in educational settings, often measured by tests and assessments designed to evaluate one's learning potential or intellectual ability.