Solved

Let Y Be a Bernoulli Random Variable with Success Probability

question 53

Essay

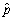Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let $Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let be the fraction of successes (1s)in this sample.In large samples,the distribution of will be approximately normal,i.e. , is approximately distributed N(p, ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.$ be the fraction of successes (1s)in this sample.In large samples,the distribution of $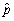Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let be the fraction of successes (1s)in this sample.In large samples,the distribution of will be approximately normal,i.e. , is approximately distributed N(p, ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.$ will be approximately normal,i.e. 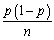, $Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let be the fraction of successes (1s)in this sample.In large samples,the distribution of will be approximately normal,i.e. 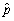, is approximately distributed N(p, ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.$ is approximately distributed N(p, $Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let be the fraction of successes (1s)in this sample.In large samples,the distribution of will be approximately normal,i.e. , is approximately distributed N(p, ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.$ ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to $Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let be the fraction of successes (1s)in this sample.In large samples,the distribution of will be approximately normal,i.e. , is approximately distributed N(p, ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.$ ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.

Definitions:

Forward Contract

A customized financial agreement to buy or sell an asset at a specified future date at a price agreed upon today.

Future Date

A specified day in the future, often used in the context of agreements or financial transactions that will occur at a later time.

Amortized Historical Cost

The accounting method of gradually writing off the initial cost of an asset over a period, adjusting for depreciation or amortization.

Market Value

The present listed price for purchasing or selling an asset or service in a market.