During the last few days before a presidential election,there is a frenzy of voting intention surveys.On a given day,quite often there are conflicting results from three major polls.
(a)Think of each of these polls as reporting the fraction of successes (1s)of a Bernoulli random variable Y,where the probability of success is Pr(Y = 1)= p.Let 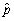 be the fraction of successes in the sample and assume that this estimator is normally distributed with a mean of p and a variance of
be the fraction of successes in the sample and assume that this estimator is normally distributed with a mean of p and a variance of  .Why are the results for all polls different,even though they are taken on the same day?
.Why are the results for all polls different,even though they are taken on the same day?
(b)Given the estimator of the variance of 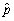 ,
, 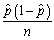 ,construct a 95% confidence interval for
,construct a 95% confidence interval for 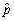 .For which value of
.For which value of 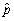 is the standard deviation the largest? What value does it take in the case of a maximum
is the standard deviation the largest? What value does it take in the case of a maximum 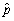 ?
?
(c)When the results from the polls are reported,you are told,typically in the small print,that the "margin of error" is plus or minus two percentage points.Using the approximation of 1.96 ≈ 2,and assuming,"conservatively," the maximum standard deviation derived in (b),what sample size is required to add and subtract ("margin of error")two percentage points from the point estimate?
(d)What sample size would you need to halve the margin of error?
Definitions:
Biological Factors
Refer to physiological, genetic, and neurological conditions that affect an individual's behavior and traits.
Social Factors
Aspects of society that influence individuals' behaviors, attitudes, and life chances.
Life Span
The maximum or average duration of life of an organism or a category of organisms.
Personality Develops
The process by which an individual's characteristic patterns of thinking, feeling, and behaving are established and change over time.
Q6: Assume that var(ui|Xi)= θ0+θ1 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="Assume
Q9: If Xt and Yt are cointegrated,then the
Q15: Your textbook estimates the initial relationship between
Q24: Your professor wants to measure the class's
Q27: (Requires some calculus)In the following,assume that Xt
Q29: Consider the distributed lag model Yt =
Q37: In the expression Pr(deny = 1 <img
Q40: When the target duration is set at
Q50: Using the California School data set from
Q56: Assume that you had estimated the following