Examlex

Solved

(Advanced)Unbiasedness and Small Variance Are Desirable Properties of Estimators

question 33

Essay

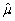(Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of "mean square error" estimator combines the two concepts.Let (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. 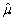) be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. 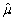) )= E( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. 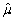) - μ)2.Prove that MSE( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. 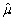) )= bias2 + var( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. ) ).(Hint: subtract and add in E( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. ) )in E( (Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of mean square error estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( - μ)2.Prove that MSE( )= bias2 + var( ).(Hint: subtract and add in E( )in E( - μ)2. ) - μ)2. )

Definitions:

Status

The social or professional standing or rank of an individual or thing.

Ranking

The hierarchy or order of items according to their importance, quality, performance, etc.

Insecurity

A feeling of uncertainty or anxiety about oneself; a lack of confidence.

Personal Feelings

Individual emotions or sentiments that are subjective and internal to one's self.

Related Questions

Q9: (Requires Calculus)For the simple linear regression model

Q20: Assume the following model of the labor

Q34: The central limit theorem<br>A)states conditions under which

Q35: A large p-value implies<br>A)rejection of the null

Q41: Assume that under the null hypothesis, <img

Q43: A VAR with k time series variables

Q50: Indicate for which of the following examples

Q55: The following statement about the sample correlation

Q60: To standardize a variable you<br>A)subtract its mean

Q61: (Requires Statistics background beyond Chapters 2 and