The Following Problem Is Frequently Encountered in the Case of a Rare

question 68

Essay

The following problem is frequently encountered in the case of a rare disease,say AIDS,when determining the probability of actually having the disease after testing positively for HIV.(This is often known as the accuracy of the test given that you have the disease. )Let us set up the problem as follows: Y = 0 if you tested negative using the ELISA test for HIV,Y = 1 if you tested positive;X = 1 if you have HIV,X = 0 if you do not have HIV.Assume that 0.1 percent of the population has HIV and that the accuracy of the test is 0.95 in both cases of (i)testing positive when you have HIV,and (ii)testing negative when you do not have HIV.(The actual ELISA test is actually 99.7 percent accurate when you have HIV,and 98.5 percent accurate when you do not have HIV. )
(a)Assuming arbitrarily a population of 10,000,000 people,use the accompanying table to first enter the column totals.
(b)Use the conditional probabilities to fill in the joint absolute frequencies.
(c)Fill in the marginal absolute frequencies for testing positive and negative.Determine the conditional probability of having HIV when you have tested positive.Explain this surprising result.
(d)The previous problem is an application of Bayes' theorem,which converts Pr(Y = y 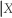= x)into Pr(X = x = y).Can you think of other examples where Pr(Y = y 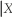= x)≠ Pr(X = x 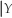= y)?

---

Definitions:

Egocentrism

A cognitive characteristic where an individual has difficulty understanding or acknowledging a perspective other than their own.

Narcissism

A personality trait characterized by an exaggerated sense of self-importance, need for admiration, and lack of empathy for others.

Disparity

A great difference or inequality between two or more things, often leading to an unfair situation.

Preoperational

The stage in Jean Piaget's theory of cognitive development where children (aged 2 to 7) begin to engage in symbolic play and struggle with logic and taking the perspective of others.