The Following Problem Is Frequently Encountered in the Case of a Rare

question 68

Essay

The following problem is frequently encountered in the case of a rare disease,say AIDS,when determining the probability of actually having the disease after testing positively for HIV.(This is often known as the accuracy of the test given that you have the disease. )Let us set up the problem as follows: Y = 0 if you tested negative using the ELISA test for HIV,Y = 1 if you tested positive;X = 1 if you have HIV,X = 0 if you do not have HIV.Assume that 0.1 percent of the population has HIV and that the accuracy of the test is 0.95 in both cases of (i)testing positive when you have HIV,and (ii)testing negative when you do not have HIV.(The actual ELISA test is actually 99.7 percent accurate when you have HIV,and 98.5 percent accurate when you do not have HIV. )
(a)Assuming arbitrarily a population of 10,000,000 people,use the accompanying table to first enter the column totals.
(b)Use the conditional probabilities to fill in the joint absolute frequencies.
(c)Fill in the marginal absolute frequencies for testing positive and negative.Determine the conditional probability of having HIV when you have tested positive.Explain this surprising result.
(d)The previous problem is an application of Bayes' theorem,which converts Pr(Y = y 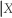= x)into Pr(X = x = y).Can you think of other examples where Pr(Y = y 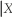= x)≠ Pr(X = x 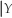= y)?

---

Definitions:

Facial Feedback

The hypothesis that facial movements can influence emotional experiences, suggesting that expressions can contribute to feelings.

Basic Emotion

Fundamental emotions that are hard-wired into the brain and universally recognized, such as happiness, sadness, fear, and anger.

Visual Cliff

A psychological experiment setup to test infants' and young animals' perception of depth and their fear of falling.

Ambiguous

Something that can be understood in more than one way or is unclear because it has multiple interpretations.