Examlex

Solved

Define the GLS Estimator and Discuss Its Properties When Ω

question 25

Essay

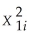Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui Xi)= ch(Xi)= σ2 ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into = FU,and F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data. 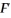Xi)= ch(Xi)= σ2 Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui Xi)= ch(Xi)= σ2 ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into = FU,and F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data. ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui Xi)= ch(Xi)= σ2 ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into = FU,and F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data. = FU,and Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui Xi)= ch(Xi)= σ2 ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into = FU,and F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data. F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data.

Definitions:

Budgeted Capacity

The amount of production or activity level planned for a future period, based on budget allocations.

Practical Capacity

The maximum amount of work or output that can be realistically achieved in a specific period under normal operating conditions.

Cost Allocation

The process of assigning indirect costs to different departments, products, or projects based on relevant distribution bases.

Cost Pool

A grouping of individual costs, typically by department or service center, from which cost allocations are made.

Related Questions

Q18: The net weight of a bag of

Q26: The OLS estimator<br>A)has the multivariate normal asymptotic

Q41: Below you are asked to decide on

Q42: In a simple regression with an intercept

Q43: Being a competitive female swimmer,you wonder if

Q46: Experimental data are often<br>A)observational data.<br>B)binary data,in that

Q48: The sample regression line estimated by OLS<br>A)has

Q49: A nonlinear function<br>A)makes little sense,because variables in

Q65: In a multiple regression framework,the slope coefficient

Q119: The sum of the column percents in