(Requires Appendix Material)If the Gauss-Markov Conditions Hold,then OLS Is BLUE

question 24

Essay

(Requires Appendix material)If the Gauss-Markov conditions hold,then OLS is BLUE.In addition,assume here that X is nonrandom.Your textbook proves the Gauss-Markov theorem by using the simple regression model Yi = β0 + β1Xi + ui and assuming a linear estimator 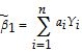.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 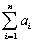= 0 and 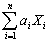= 1.
The variance of the estimator is var( X1,…,Xn)= .
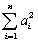Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.

---

Definitions:

Social Identity

An individual’s sense of self derived from perceived membership in social groups, which shapes self-concept and behavior in group contexts.

Speech Elocution

The skill or art of clear and expressive speech, including the production of distinct sounds and the proper use of tone, pitch, and pace.

Social Mobility Belief System

The set of beliefs and values about the ability of individuals to move within or between social strata or classes.

Higher-Status Group

A social group considered to possess greater prestige, privileges, or authority within a given context or society.