(Requires Appendix Material)If the Gauss-Markov Conditions Hold,then OLS Is BLUE

question 24

Essay

(Requires Appendix material)If the Gauss-Markov conditions hold,then OLS is BLUE.In addition,assume here that X is nonrandom.Your textbook proves the Gauss-Markov theorem by using the simple regression model Yi = β0 + β1Xi + ui and assuming a linear estimator 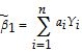.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 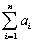= 0 and 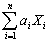= 1.
The variance of the estimator is var( X1,…,Xn)= .
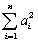Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.

---

Definitions:

Congenital

A condition or trait present from birth, which can result from genetic factors or environmental influences during pregnancy.

Malformation

An abnormality in the formation, shape, or structure of a part of the body, often present from birth.

Preexisting

Already existing before a specified point in time or before an analysis, event, or assessment.

Amniocentesis

A medical procedure used in prenatal diagnosis where a small amount of amniotic fluid is sampled from the amniotic sac around a developing fetus.