Examlex

Solved

Consider the Standard AR(1)Yt = β0 + β1Yt-1 + Ut,where

question 21

Essay

Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold.
(a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0.
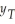(b)Show that the r-period ahead forecast E( Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . 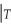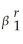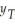+r Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . 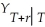)= Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . for large r?
(c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . +r Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . )= 0.5 Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r 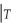)= 0.5 .Show that in the present case this is given by r = - . .Show that in the present case this is given by r = - Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . .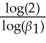

Definitions:

General Damages

Compensation awarded for non-monetary losses suffered due to a breach of contract or tort, such as pain and suffering or loss of reputation.

Incidental Damages

Financial losses indirectly resulting from a party's failure to meet a contractual obligation.

Trade Secrets

Confidential business information that provides an enterprise a competitive edge and is protected from disclosure by law.

Trademarks

Recognizable signs, designs, or expressions that distinguish the products or services of a particular trader from those of others.

Related Questions

Q13: The accompanying table lists the height (STUDHGHT)in

Q18: The net weight of a bag of

Q24: You have analyzed the relationship between the

Q24: You collect monthly data on the money

Q30: In the distributed lag model,the coefficient on

Q40: A VAR with five variables,4 lags and

Q44: The student newspaper called Campus Press polled

Q60: When testing for differences of means,you can

Q78: The large-sample significance test for population proportion

Q80: Give a definition for meta-analysis.