You Have a Limited Dependent Variable (Y)and a Single Explanatory

question 41

Essay

You have a limited dependent variable (Y)and a single explanatory variable (X).You estimate the relationship using the linear probability model,a probit regression,and a logit regression.The results are as follows: 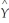= 2.858 - 0.037 × X
(0.007)
Pr(Y = 1 X)= F (15.297 - 0.236 × X)
Pr(Y = 1 X)= Φ (8.900 - 0.137 × X)
(0.058)
(a)Although you cannot compare the coefficients directly,you are told that "it can be shown" that certain relationships between the coefficients of these models hold approximately.These are for the slope: 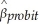≈ 0.625 × , ≈ 0.25 × 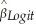.Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
(b)For the intercept,the same conversion holds for the logit-to-probit transformation.However,for the linear probability model,there is a different conversion: 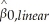≈ 0.2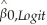5 × + 0.5
Using the logit regression as the base,calculate a few changes in X (temperature in degrees of Fahrenheit)to see how good the approximations are.

---

Definitions:

Motionless Body

Describes a state of not moving or being completely still.

Terrorist Bombing

The use of explosive devices by terrorists to cause disruption, fear, injury, or death, typically targeting civilians to achieve political ends.

Day-To-Day Happiness

The experience of joy, contentment, or positive well-being on a regular, daily basis.

Subjective Well-Being

A person's self-evaluation of their total contentment and fulfillment in life.