Two authors published a study in 1992 of the effect of minimum wages on teenage employment using a U.S.state panel.The paper used annual observations for the years 1977-1989 and included all 50 states plus the District of Columbia.The estimated equation is of the following type
(Eit )= β0 + β1 (Mit /Wit )+ 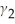 D2i + ...+
D2i + ...+ 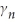 D51i +
D51i +  B2t + ...+
B2t + ...+  B13t + uit,
B13t + uit,
where E is the employment to population ratio of teenagers,M is the nominal minimum wage,and W is average wage in the state.In addition,other explanatory variables,such as the prime-age male unemployment rate,and the teenage population share were included.
(a)Briefly discuss the advantage of using panel data in this situation rather than pure cross sections or time series.
(b)Estimating the model by OLS but including only time fixed effects results in the following output 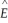 it =
it = 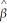 0 - 0.33 × (Mit /Wit )+ 0.35(SHYit)- 1.53 × uramit;R2 = 0.20
0 - 0.33 × (Mit /Wit )+ 0.35(SHYit)- 1.53 × uramit;R2 = 0.20
(0.08)(0.28)(0.13)
where SHY is the proportion of teenagers in the population,and uram is the prime-age male unemployment rate.Coefficients for the time fixed effects are not reported.Numbers in parenthesis are homoskedasticity-only standard errors.
Comment on the above results.Are the coefficients statistically significant? Since these are level regressions,how would you calculate elasticities?
(c)Adding state fixed effects changed the above equation as follows: 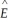 it =
it = 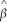 0 + 0.07 × (Mit /Wit )- 0.19 × (SHYit)- 0.54 × uramit;
0 + 0.07 × (Mit /Wit )- 0.19 × (SHYit)- 0.54 × uramit; 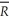 2 = 0.69
2 = 0.69
(0.10)(0.22)(0.11)
Compare the two results.Why would the inclusion of state fixed effects change the coefficients in this way?
(d)The significance of each coefficient decreased,yet 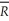 2 increased.How is that possible? What does this result tell you about testing the hypothesis that all of the state fixed effects can be restricted to have the same coefficient? How would you test for such a hypothesis?
2 increased.How is that possible? What does this result tell you about testing the hypothesis that all of the state fixed effects can be restricted to have the same coefficient? How would you test for such a hypothesis?
Definitions:
Income Distributions
Payments, often periodic, received by investors from assets they own, such as dividends from stocks or interest from bonds.
Rate of Return
The increase or decrease in the value of an investment during a set period, represented as a proportion of the investment's original price.
Income Distributions
Payments made to investors from the earnings derived from the investments within a fund, such as dividends or interest payments.
Q5: The accompanying graph <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="The accompanying
Q8: Consider the following linear transformation of a
Q15: If you included both time and entity
Q17: A test of significance can be used
Q26: Your textbook mentions heteroskedasticity- and autocorrelation- consistent
Q32: If the data are not normal and
Q45: Calculate the following probabilities using the standard
Q49: To test for randomization when Xi is
Q75: A simple random sample of 100 college
Q91: The alternative hypothesis H<sub>a</sub> in a two-way