Two Dentists, Lydia Russell and Jerry Carlton, Are Planning to Establish

question 194

Essay

Two dentists, Lydia Russell and Jerry Carlton, are planning to establish practices in a newly developed community. Both have allocated approximately the same total budget for advertising in the local newspaper and for the distribution of fliers announcing their practices. Because of the location of their offices, Russell is expected to get 47% of the business if both dentists advertise only in the local newspaper; if both dentists advertise through fliers, then Russell is expected to get 44% of the business; if Russell advertises exclusively in the local newspaper and Carlton advertises exclusively through fliers, then Russell is expected to get 61% of the business. Finally, if Russell advertises through fliers exclusively and Carlton advertises exclusively in the local newspaper, then Russell is expected to get 50% of the business.
Construct the payoff matrix for the game. 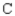C = Carlton; R = Russell
N = local newspaper; F = flyer 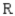Is the game strictly determined?
Find the optimal strategy for both Russell and Carlton.
Please round the answer to the nearest hundredth.

---

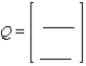
Definitions:

Public Sector

The part of the economy composed of both public services and public enterprises, owned and operated by the government.

Generate Revenue

The process of producing income through sales of products, services, or other mechanisms within a business.

Compensation Survey

A tool used by organizations to gather and analyze competitive salary information in order to determine appropriate compensation levels for their employees.

Compensation System

The overall structure and methodology an organization uses to compensate its employees, including wages, salaries, benefits, and incentives.