Consider the production problem: One company wishes to produce two types of souvenirs: type A and type B. Each type-A souvenir will result in a profit of $1, and each type-B souvenir will result in a profit of $1.2. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II.There are 180 minutes available on machine I and 300 minutes available on machine II for processing the order.
Maximaze  Objective function
Objective function
Subject to 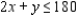 Constrained 1
Constrained 1  Constrained 2
Constrained 2 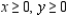 Now suppose the time available on machine I is changed from 180 minutes to (180 + h) minutes, where h is a real number. Then the constraint on machine I is changed to
Now suppose the time available on machine I is changed from 180 minutes to (180 + h) minutes, where h is a real number. Then the constraint on machine I is changed to 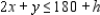 But the line with equation
But the line with equation 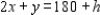 is parallel to the line
is parallel to the line 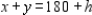 associated with the original constraint 1.
associated with the original constraint 1.
As you can see from the figure , the result of adding the constant h to the right-hand side of constraint 1 is to shift the current optimal solution from the point C to the new optimal solution occurring at the point C. To find the coordinates of C, we observe that C is the point of intersection of the lines with equations  Thus, the coordinates of the point are found by solving the system of linear equations
Thus, the coordinates of the point are found by solving the system of linear equations 
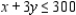
 The solutions are
The solutions are 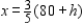 and
and 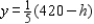 The nonnegativity of x implies that
The nonnegativity of x implies that 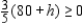
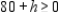
 Next, the nonnegativity of y implies that
Next, the nonnegativity of y implies that 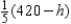

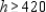 Thus, h must satisfy the inequalities
Thus, h must satisfy the inequalities 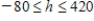 . Computations reveal that for a meaningful solution the time available for machine I must range between (180 - 80) and (180 + 420) minutes-that is, between 100 and 600 minutes.
. Computations reveal that for a meaningful solution the time available for machine I must range between (180 - 80) and (180 + 420) minutes-that is, between 100 and 600 minutes.
According to the problem, optimal solution would be 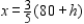 and
and 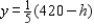 The resulting profit is calculated as follows:
The resulting profit is calculated as follows: 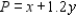
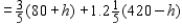
 Upon setting h = 1, we find
Upon setting h = 1, we find 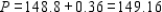 Since the optimal profit for the original problem is $159.6, we see that the shadow price for the first resource is 149.16 - 148.80, or $.36.
Since the optimal profit for the original problem is $159.6, we see that the shadow price for the first resource is 149.16 - 148.80, or $.36.
Show that if the time available on machine II is changed from 300 min to (300 + k) min, with no change in the maximum capacity for machine I, then company profit is maximized by producing 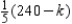 type-A souvenirs and
type-A souvenirs and 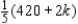 type-B souvenirs, where
type-B souvenirs, where 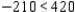 .
.
Definitions:
Streetwalking
The act of soliciting sexual services in public places, typically for money.
Sexually Assaulted
The act of subjecting someone to unwanted or forced sexual contact or activity.
Fellatio
Oral stimulation of the penis.
Psychological State
Refers to the mental condition of an individual at a specific time, influenced by emotions, thoughts, behaviors, and general mental health.
Q11: A dietitian wishes to plan a meal
Q75: Which point has a negative x-coordinate and
Q85: Find the pivot element to be used
Q115: Find the sum of the odd integers
Q170: Given that the augmented matrix in row-reduced
Q176: A finance company has a total of
Q186: A country is not building many nuclear
Q205: Robin, who is self-employed, contributes $5,500/year into
Q216: Solve the linear system of equations
Q237: Find an equation of the circle that