Solved

TABLE 13-12
the Manager of the Purchasing Department of a Large

question 96

True/False

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { ations } & 30 \\\hline\end{array}\end{array}$

$\begin{array}{lrrccc}\hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\\hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\\hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$

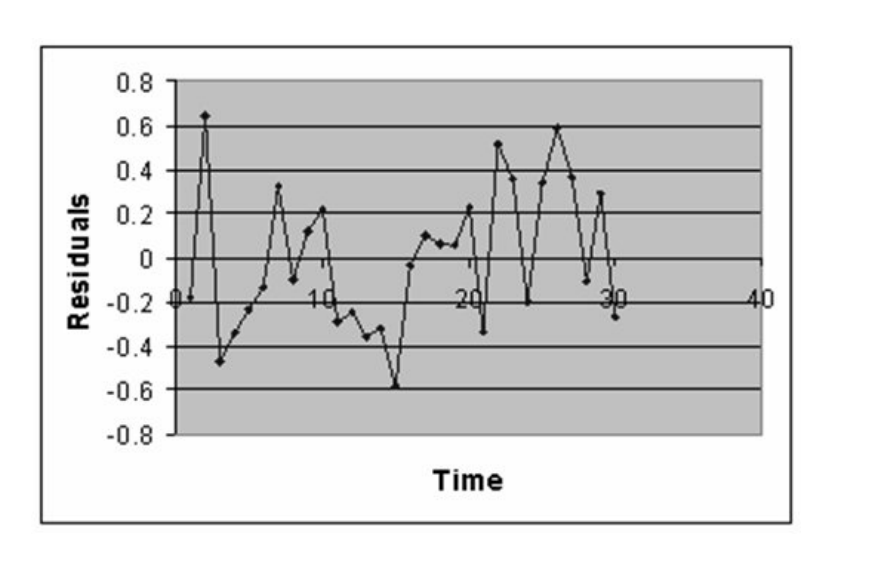
$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, there is sufficient evidence that the amount of time needed linearly depends on the number of invoices processed at a 1% level of significance.$

$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, there is sufficient evidence that the amount of time needed linearly depends on the number of invoices processed at a 1% level of significance.$

-Referring to Table 13-12, there is sufficient evidence that the amount of time needed linearly depends on the number of invoices processed at a 1% level of significance.

Learn the significance of linear programming in optimizing production and pricing strategies amidst resource constraints.

Understand the role of legislation in guiding commercial activities including pricing.

Comprehend the distinctions and applications of various pricing strategies such as skimming, penetration, and predatory pricing.

Understand how contribution margin analysis and cost allocation affect pricing and production decisions.

Definitions:

Collective Action

The action taken together by a group of people whose goal is to enhance their status and achieve a common objective.

Social Protest

A collective action or demonstration expressing opposition to, or support for, a cause, policy, or set of conditions.

Collective Behaviour

The behaviour of people en masse – such as in a crowd, protest or riot.

Uniform Manner

Acting or executing in a consistent and identical way across different situations or instances.

TABLE 13-12 the Manager of the Purchasing Department of a Large

Definitions:

TABLE 13-12
the Manager of the Purchasing Department of a Large