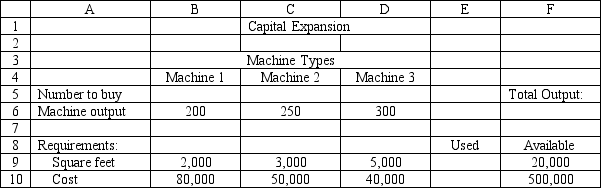
A Company Needs to Purchase Several New Machines to Meet $\quad \mathbf { x } _ { \mathrm { i } } =$

question 26

Essay

A company needs to purchase several new machines to meet its future production needs. It can purchase three different types of machines A, B, and C. Each machine A costs $80,000 and requires 2,000 square feet of floor space. Each machine B costs $50,000 and requires 3,000 square feet of floor space. Each machine C costs $40,000 and requires 5,000 square feet of floor space. The machines can produce 200, 250 and 350 units per day respectively. The plant can only afford $500,000 for all the machines and has at most 20,000 square feet of room for the machines. The company wants to buy as many machines as possible to maximize daily production.
What values would you enter in the Risk Solver Platform (RSP) task pane for the following cells for this Excel spreadsheet implementation of the formulation for this problem?
Objective Cell:
Variables Cells:
Constraints Cells:
Let $\quad \mathbf { x } _ { \mathrm { i } } =$ mumber of machines of type i purchased

$\begin{array}{ll}\text { MAX: } & 200 \mathrm{X}_{1}+250 \mathrm{X}_{2}+300 \mathrm{X}_{3} \\\text { Subject to: } & 2 \mathrm{X}_{1}+3 \mathrm{X}_{2}+5 \mathrm{X}_{3} \leq 20 \\& 80 \mathrm{X}_{1}+50 \mathrm{X}_{2}+40 \mathrm{X}_{3} \leq 500 \\& \mathrm{X}_{1}, \mathrm{X}_{3} \mathrm{X}_{3} \geq 0\end{array}$

---

Definitions:

Splenic Vein

A vein that drains blood from the spleen, pancreas, and portions of the stomach, emptying into the portal vein.

Hepatic Portal Vein

A blood vessel that carries nutrient-rich blood from the gastrointestinal tract and spleen to the liver for processing.

Osmotic Pressure

The pressure required to prevent the flow of a solvent across a semipermeable membrane, which separates solutions of different concentrations.

Hydrostatic Pressure

The force caused by gravity that a stationary fluid exerts.