A financial planner wants to design a portfolio of investments for a client. The client has $400,000 to invest and the planner has identified four investment options for the money. The following requirements have been placed on the planner. No more than 30% of the money in any one investment, at least one half should be invested in long-term bonds which mature in six or more years, and no more than 40% of the total money should be invested in B or C since they are riskier investments. The planner has developed the following LP model based on the data in this table and the requirements of the client. The objective is to maximize the total return of the portfolio.
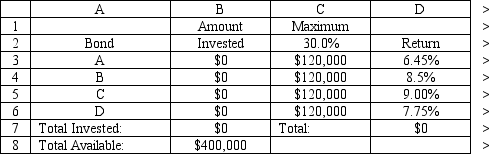
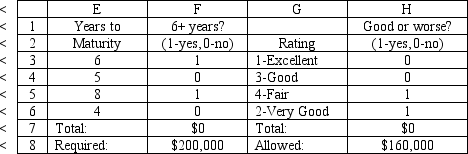 What formulas are required for the following cells in the Excel spreadsheet implementation of the formulation?
What formulas are required for the following cells in the Excel spreadsheet implementation of the formulation?
B7
D7
F7
H7
Definitions:
Housing
The creation and allocation of living spaces for individuals and families, considered essential for well-being and social stability.
Treatment Groups
Groups formed with the purpose of providing therapy, support, or interventions to individuals sharing common issues or conditions.
Resolve Problems
Resolving problems entails finding solutions to issues or difficulties encountered within various contexts, such as personal, professional, or societal.
Q2: A railroad needs to move the maximum
Q2: In the past, battlefield surgery was crude
Q3: Refer to Exhibit 10.1. Based on the
Q21: A company is developing its weekly
Q42: Refer to Exhibit 7.2. Which cell(s) is(are)
Q43: Refer to Exhibit 3.2. Which cells should
Q51: Implementing solutions to problems involves people and
Q62: The setup cost incurred in preparing a
Q67: How is the integer tolerance factor set
Q75: Refer to Exhibit 9.3. Predict the mean