An Investor Has $500,000 to Invest and Wants to Maximize

question 11

Essay

An investor has $500,000 to invest and wants to maximize the money they will receive at the end of one year. They can invest in condos, apartments and houses. The profit after one year, the cost and the number of units available are shown below.
$\begin{array}{clccc}&& \text { Profit } & \text { Cost } & \text { Number}\\\text { Variable } & \text { Investment } & (\$ 1,000) & (\$ 1,000) & \text { Available } \\\hline \mathrm{X}_{1} & \text { Condos } & 6 & 50 & 10 \\\mathrm{X}_{2} & \text { Apartments } & 12 & 90 & 5 \\\mathrm{X}_{3} & \text { Houses } & 9 & 100 & 7\end{array}$
Based on this ILP formulation of the problem and the indicated optimal integer solution values what values should go in cells B5:F12 of the following Excel spreadsheet?
MAX: $\quad 6 \mathbf { X } _ { 1 } + 12 \mathbf { X } _ { \mathbf { 2 } } + 9 \mathbf { X } _ { \mathbf { 3 } }$
Subject to:
$\begin{array} { l } 50 X _ { 1 } + 90 X _ { \mathbf { 2 } } + 100 X _ { \mathbf { 3 } } \leq 500 \\\mathbf { X } _ { 1 } \leq 10 \\\mathbf { X } _ { \mathbf { 2 } } \leq 5 \\\mathbf { X } _ { \mathbf { 3 } } \leq 7 \\\mathbf { X } _ { \mathrm { i } } \geq 0 \text { and integer }\end{array}$
Salution: 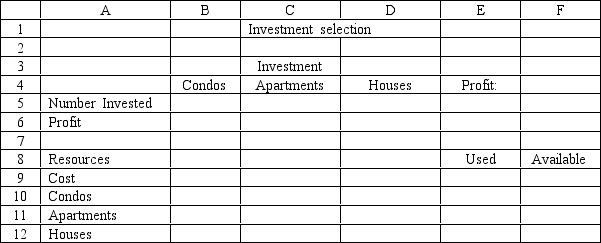$\left( \mathbf { X } _ { 1 } , \mathbf { X } _ { 2 } \mathbf { X } _ { \mathbf { 3} } \right) = ( 1,5, 0)$

---

Definitions:

Buying Price

The cost at which an individual or organization is able to purchase a good, service, or asset.

Oligopsony

Market with only a few buyers.

Buying Price

The price at which a good or service is purchased by a consumer or another business.

Marginal Value Curve

The marginal value curve represents how the value of the last unit consumed (marginal value) changes as the quantity consumed increases.