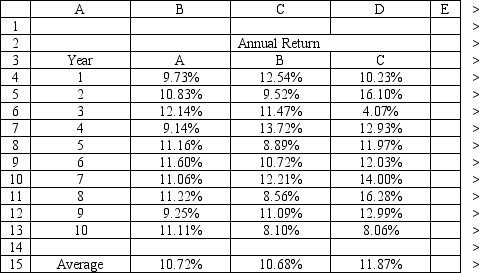
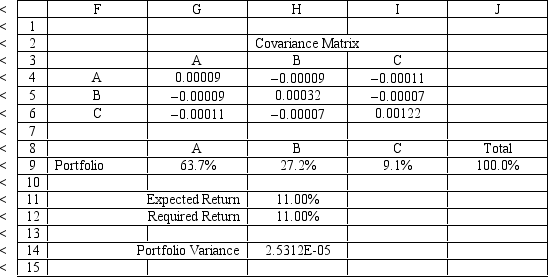
An Investor Is Developing a Portfolio of Stocks $\quad 0.00009 \mathrm{P}_{1}^{2}+0.00032 \mathrm{P}_{2}^{2}+0.00122 \mathrm{P}_{3}^{2}$

question 64

Essay

An investor is developing a portfolio of stocks. She has identified 3 stocks in which to invest. She wants to earn at least 11% return but with minimum risk.
Let: P_i = proportion of total funds invested in i, i = A, B, C
The NLP for this problem is:
MIN: $\quad 0.00009 \mathrm{P}_{1}^{2}+0.00032 \mathrm{P}_{2}^{2}+0.00122 \mathrm{P}_{3}^{2}$
$+2\left(-0.00009 \mathrm{P}_{1} \mathrm{P}_{2}-0.00011 \mathrm{P}_{1} \mathrm{P}_{3}-0.00007 \mathrm{P}_{2} \mathrm{P}_{3}\right. )$

Subject to:
$\begin{array}{l}P_{1}+P_{2}+P_{3}=1 \\0.1072 P_{1}+0.1068 P_{2}+0.1187 P_{3} \geq 0.11 \\P_{1}, P_{2}, P_{3} \geq 0 \\P_{1}, P_{2}, P_{3} \leq 1\end{array}$
What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.

---

Definitions:

Breach

The violation of a law, duty, or other form of agreement, resulting in an actionable grievance.

Strobe-Light Image

A visual effect produced by rapid flashes of light, creating a series of frozen images of moving objects.

Specific Intent

A legal term indicating that an individual had a particular purpose or objective in mind when committing an act, especially relevant in criminal law.

Legal Duty

An obligation established by law that requires an individual or entity to conform to a certain standard of conduct.