TABLE 15-9
Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected.
ATTENDANCE = Paid attendance for the game
TEMP = High temperature for the day
WIN% = Team's winning percentage at the time of the game
OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held
The regression results using attendance as the dependent variable and the remaining five variables as the independent variables are presented below.
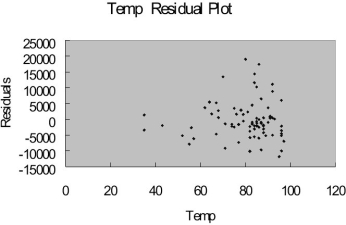
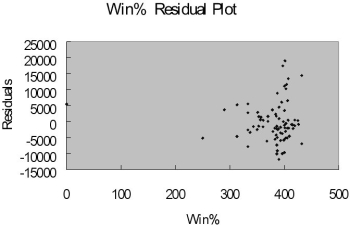
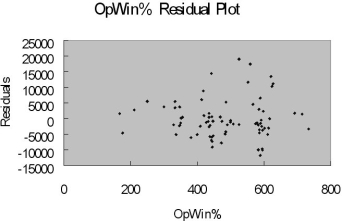
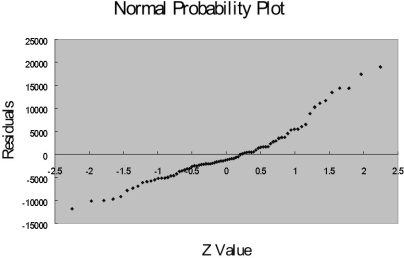
The coefficient of multiple determination ( R 2 j ) of each of the 5 predictors with all the other remaining predictors are,
respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308.
-Referring to Table 15-9, what is the value of the test statistic to determine whether TEMP makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
Definitions:
Interim Financial Reporting
Reporting of a company's financial performance and position for a period shorter than its fiscal year, often quarterly.
Statement Of Cash Flows
A financial report that provides a summary of a company's cash inflows and outflows over a specified period, showing how well it manages its cash position.
Operating Segment
A component of a company that engages in business activities from which it may earn revenues and incur expenses, and about which separate financial information is available.
Reportable Segment
A component of an enterprise that is distinguished by business activities, geographical areas, or products and services, requiring separate financial disclosure under accounting standards.
Q33: Referring to Table 13-4, suppose the managers
Q42: Referring to Table 18-4, suppose the supervisor
Q46: Using the Cp statistic in model building,
Q52: Referring to Table 16-11, the residuals for
Q62: Using the best-subsets approach to model building,
Q128: Referring to Table 14-17, what is the
Q129: If the Durbin-Watson statistic has a value
Q147: Referring to Table 13-2, what is the
Q189: Referring to Table 13-11, there is sufficient
Q190: Referring to Table 16-9, the forecast for