Solved

TABLE 13-12
the Manager of the Purchasing Department of a Large

question 92

Multiple Choice

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$\begin{array}{lc}\text { Regression Statistics } \\\hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { Observations } & 30\end{array}$

$\text { ANOVA }$
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Significance } F \\\text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coeffcients } & \text { StandardError } & t \text { Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Invoices } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Processed } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$
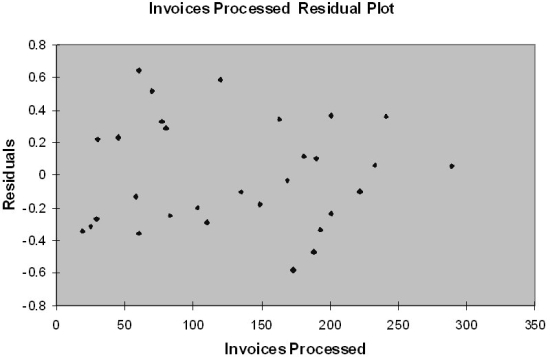
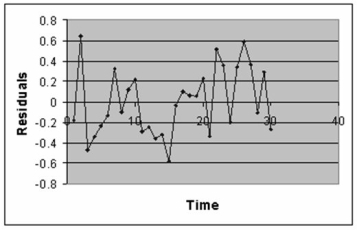
$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{lc} \text { Regression Statistics } \\ \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { Observations } & 30 \end{array} \text { ANOVA } \begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Significance } F \\ \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coeffcients } & \text { StandardError } & t \text { Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Invoices } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text { Processed } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the degrees of freedom for the F test on whether the number of invoices processed affects the amount of time are A) 1, 29. B) 28, 1. C) 29, 1. D) 1, 28.$ $TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{lc} \text { Regression Statistics } \\ \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { Observations } & 30 \end{array} \text { ANOVA } \begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Significance } F \\ \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coeffcients } & \text { StandardError } & t \text { Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Invoices } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text { Processed } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the degrees of freedom for the F test on whether the number of invoices processed affects the amount of time are A) 1, 29. B) 28, 1. C) 29, 1. D) 1, 28.$
-Referring to Table 13-12, the degrees of freedom for the F test on whether the number of invoices processed affects the amount of time are

Definitions:

Radical Scavenger

A molecule that can donate an electron to a free radical without becoming a radical itself, effectively neutralizing the free radical.

Resonance Stabilized

A molecule or ion that is stabilized by the delocalization of electrons across different structures or resonance forms.

Free Radical Bromination

A chemical reaction where bromine radicals selectively react with hydrogen atoms in an organic molecule to form brominated products.

1-Bromopentane

An alkyl halide with the formula C5H11Br, used in organic synthesis as an alkylating agent.

TABLE 13-12 the Manager of the Purchasing Department of a Large

Definitions:

TABLE 13-12
the Manager of the Purchasing Department of a Large