TABLE 13- 11
A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles:
ANOVA
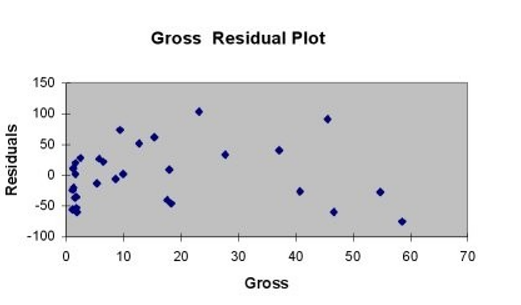

-Referring to Table 13-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between box office gross and home video unit sales?
Definitions:
AVC
Average Variable Cost represents the variable costs (like materials and labor) associated with producing each unit of output.
ATC
Average Total Cost, the total cost of production divided by the quantity of output produced, encompassing both fixed and variable costs.
MC
Short for Marginal Cost, it refers to the change in total cost that arises when the quantity produced is incremented by one unit.
MR
Marginal Revenue, the additional income that is gained from selling one more unit of a good or service.
Q5: If the assumptions of the one-way ANOVA
Q51: Which of the following is not used
Q55: In a simple linear regression problem, r
Q62: Referring to Table 13-9, to test the
Q73: Referring to Table 16-6, the Holt-Winters method
Q102: Referring to Table 13-4, the prediction for
Q112: The variation attributable to factors other than
Q148: Referring to Table 14-8, the predicted salary
Q184: Referring to Table 12-14, what type of
Q255: Referring to Table 14-10, to test the