TABLE 13-12
the Manager of the Purchasing Department of a Large

question 178

True/False

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { ations } & 30 \\\hline\end{array}\end{array}$$

$\begin{array}{lrrccc}\hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\\hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\\hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$





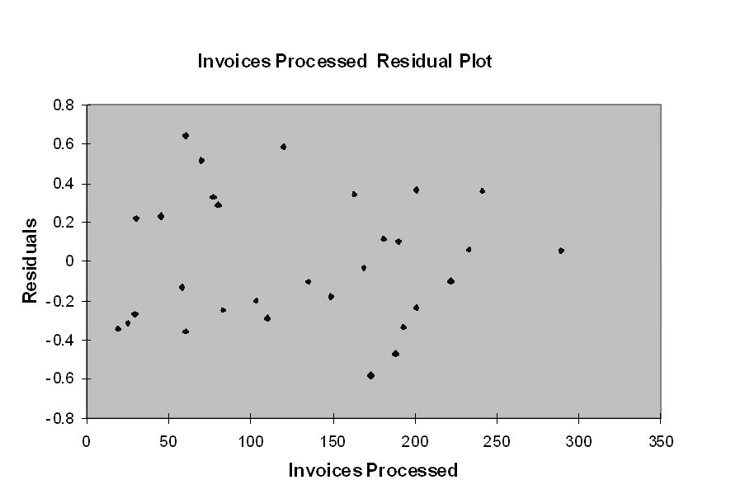
-Referring to Table 13-12, there is a 95% probability that the average amount of time needed to process one additional invoice is somewhere between 0.0109 and 0.0143 hours.

Evaluate the practices that promote fairness and dignity in the workplace.

Distinguish between different perceptions and approaches within the same occupation.

Identify the virtues exemplified by organizations and their importance.

Apply the framework of positive psychology to enhance personal well-being.

---

Definitions:

Standard Deviation

A statistic that denotes the dispersion or variability of a dataset relative to its mean, indicating how spread out the data points are.

Margin of Error

A statistic expressing the amount of random sampling error in a survey's results, indicating how much you can expect the survey results to reflect the views of the overall population.

Probability

The measure of the likelihood that a particular event will occur, expressed as a number between 0 and 1.

Standard Error

Indicates the standard deviation of the sampling distribution of a statistic, most commonly the mean.