Solved

A College Admissions Counselor Was Interested in Finding Out How

question 7

Essay

A college admissions counselor was interested in finding out how well high school grade point averages (HS GPA) predict first-year college GPAs (FY GPA). A random sample of data from first-year students was reviewed to obtain high school and first-year college GPAs. The data are shown below: $\begin{array}{|l|l|l|l|l|l|l|l|l|}\hline \text {HS GPA }& 3.82 & 3.90 & 3.20 & 3.40 & 3.88 & 3.50 & 3.60 & 3.70 \\\hline \text {FY GPA} & 3.75 & 3.45 & 2.60 & 2.95 & 3.50 & 2.76 & 3.10 & 3.40 \\\hline\end{array}$

$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text { HS GPA} & 4.00 & 3.30 & 3.50 & 3.80 & 3.87 & 4.00 & 3.20 & 3.82 \\\hline\text { FY GPA }& 3.90 & 2.70 & 3.00 & 3.00 & 3.10 & 3.77 & 2.80 & 3.54 \\\hline\end{array}$

Dependent variable is: $\quad$ FY GPA
No Selector
$\mathrm{R}$ squared $=75.4 \% \quad \mathrm{R}$ squared (adjusted) $=73.6 \%$
$s=0.2118$ with $16-2=14$ degrees of freedom

$\begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\ \text { Regression } & 1.92283 & 1 & 1.92283 & 42.9 \\ \text { Residual } & 0.627867 & 14 & 0.044848 & \\ & & & & \\ \text { Variable } & \text { Coefticient } & \text { s.e. of Coeft } & \text { t-ratio } & \text { prob } \\ \text { Constant } & -1.56410 & 0.7306 & -2.14 & 0.0504 \\ \text { HS GPA } & 1.30527 & 0.1993 & 6.55 & \leq 0.0001\end{array}$

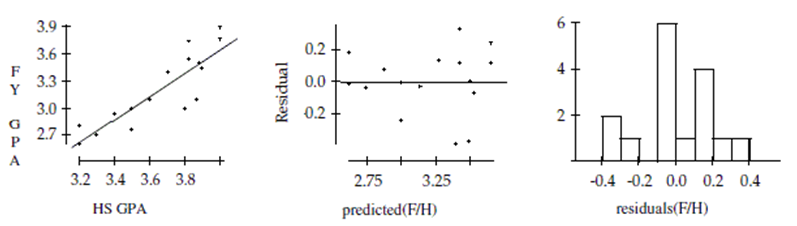
$A college admissions counselor was interested in finding out how well high school grade point averages (HS GPA) predict first-year college GPAs (FY GPA). A random sample of data from first-year students was reviewed to obtain high school and first-year college GPAs. The data are shown below: \begin{array}{|l|l|l|l|l|l|l|l|l|} \hline \text {HS GPA }& 3.82 & 3.90 & 3.20 & 3.40 & 3.88 & 3.50 & 3.60 & 3.70 \\ \hline \text {FY GPA} & 3.75 & 3.45 & 2.60 & 2.95 & 3.50 & 2.76 & 3.10 & 3.40 \\ \hline \end{array} \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline\text { HS GPA} & 4.00 & 3.30 & 3.50 & 3.80 & 3.87 & 4.00 & 3.20 & 3.82 \\ \hline\text { FY GPA }& 3.90 & 2.70 & 3.00 & 3.00 & 3.10 & 3.77 & 2.80 & 3.54 \\ \hline \end{array} Dependent variable is: \quad FY GPA No Selector \mathrm{R} squared =75.4 \% \quad \mathrm{R} squared (adjusted) =73.6 \% s=0.2118 with 16-2=14 degrees of freedom \begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\ \text { Regression } & 1.92283 & 1 & 1.92283 & 42.9 \\ \text { Residual } & 0.627867 & 14 & 0.044848 & \\ & & & & \\ \text { Variable } & \text { Coefticient } & \text { s.e. of Coeft } & \text { t-ratio } & \text { prob } \\ \text { Constant } & -1.56410 & 0.7306 & -2.14 & 0.0504 \\ \text { HS GPA } & 1.30527 & 0.1993 & 6.55 & \leq 0.0001\end{array} -Create and interpret a 95% confidence interval for the slope of the regression line.$
-Create and interpret a 95% confidence interval for the slope of the regression line.

Definitions:

Expense Recognition Principle

An accounting principle that dictates the conditions under which an expense is recognized and reported in the financial statements.

Percent of Receivables Method

An accounting technique used to estimate the amount of a company's accounts receivable that will not be collected, based on a percentage of the total accounts receivable.

Perpetual Inventory System

This is an accounting method that continuously updates inventory records for each sale or purchase of inventory.

Allowance for Doubtful Accounts

A contra-account that reduces the total receivables reported on the balance sheet to reflect the amount expected to be collected.