A Statistics Professor Investigated Some of the Factors That Affect $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$

question 93

Essay

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $X _ { 3 }$ = mid-term test mark (out of 100).
The professor recorded the data for 50 randomly selected students. The computer output is shown below.
THE REGRESSION EQUATION IS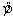
= $$41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$$ $$\begin{array} { | c | c c c | } \hline \text { Predictor } & \text { Coef } & \text { StDev } & \text { T } \\\hline \text { Constant } & 41.6 & 17.8 & 2.337 \\x _ { 1 } & - 3.18 & 1.66 & - 1.916 \\x _ { 2 } & - 1.17 & 1.13 & - 1.035 \\x _ { 3 } & 0.63 & 0.13 & 4.846 \\\hline\end{array}$$ S = 13.74 R-Sq = 30.0%. $$\begin{array}{l}\text { ANALYSIS OF VARIANCE }\\\begin{array} { | l | c c c c | } \hline \text { Source of Variation } & \text { df } & \text { SS } & \text { MS } & \text { F } \\\hline \text { Regression } & 3 & 3716 & 1238.667 & 6.558 \\\text { Error } & 46 & 8688 & 188.870 & \\\hline \text { Total } & 49 & 12404 & & \\\hline\end{array}\end{array}$$ Do these data provide enough evidence at the 1% significance level to conclude that the final mark and the mid-term mark are positively linearly related?

---

Definitions:

Symbolic Attributes

Symbolic attributes refer to the intangible qualities that imbue products or brands with meaning beyond their functional use.

Service Attributes

The inherent characteristics and features of a service that contribute to its value and quality from the perspective of the customer or user.

Physical Characteristics

The tangible attributes or features of a product or material that can be measured, such as size, shape, color, weight, and texture.

Specialty Products

Goods or services that have unique characteristics and are sought after by consumers willing to make a special effort to obtain them.