SCENARIO 14-15 the Superintendent of a School District Wanted to Predict the Predict

question 168

Multiple Choice

SCENARIO 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixthgrade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing) , mean teacher salary in thousands of dollars (Salaries) , and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = Salaries and X ₂ = Spending: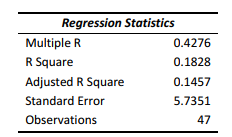


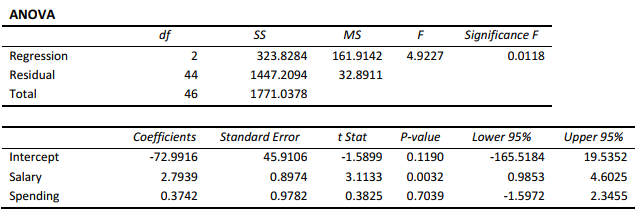
-Referring to Scenario 14-15,which of the following is a correct statement?

• A)14.57% of the total variation in the percentage of students passing the proficiency test can be explained by mean teacher salary and instructional spending per pupil.
• B)14.57% of the total variation in the percentage of students passing the proficiency test can be explained by mean teacher salary and instructional spending per pupil after adjusting for the number of predictors and sample size.
• C)14.57% of the total variation in the percentage of students passing the proficiency test can be explained by mean teacher salary holding constant the effect of instructional spending per pupil.
• D)14.57% of the total variation in the percentage of students passing the proficiency test can be explained by instructional spending per pupil holding constant the effect of mean teacher salary.

---

Definitions:

Attorney

A professional who is qualified to offer advice about the law or represent someone in legal matters.

Age at Retirement

The specific age at which an individual ceases full-time work and formally enters retirement, varying by personal choice, company policy, or statutory requirements.

Joint Frequency Distribution

A statistical method that shows the frequency of two variables occurring simultaneously within a dataset, often visualized in a table format.

Longest Run

The longest sequence of consecutive occurrences of a given outcome in a series of trials or observations.