SCENARIO 18-8
the Superintendent of a School District Wanted to Predict

question 133

True/False

SCENARIO 18-8
The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ =% Attendance, X ₂ = Salaries and X₃ = Spending: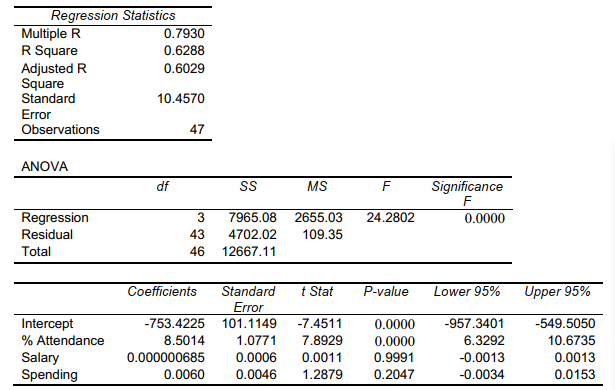

-Referring to Scenario 18-8,the null hypothesis H₀ : $\beta$ ₁ = $\beta$ ₂ = $\beta$ ₃ = 0 implies that percentage of students passing the proficiency test is not related to any of the explanatory variables.

---

Definitions:

Joint Probability Distribution

A mathematical description of the likelihood of two events occurring together and at the same point in time.

Car Salespeople

Individuals specialized in selling automobiles, often working at car dealerships.

Joint Probability Distribution

The probability distribution of two or more random variables happening simultaneously and their possible combinations.

Probability Distribution

This is a mathematic function that calculates how likely different outcomes are to occur in an experiment.