At a recent music concert, a survey was conducted that asked a random sample of 20 people their age and how many concerts they have attended since the beginning of the year. The following data were collected. Age Number of concerts 626575404493675545432656543411 Age Number of Concerts 443482554605594635694402381523 SUMMARY OUTPUT Reqression Statiatics Multiple R R Square Adjusted R Square Standard Error Observations 0.802030.643260.623440.9396520 DESCRIPTIVE STATISTICS Age Mean Standard Error Standard Deviation Sample Variance Count 532.18499.771195.473720 Concerts Mean Standard Error Standard Deviation Sample Variance Count 3.650.34241.53132.344720
SPEARMAN RANK CORRELATION COEFFICIENT =0.8306
ANOVA Regression Residual Total df 11819 SS 28.6571115.8928944.55 MS 28.657110.88294F32.45653 Significance F 2.1082E−05
Intercept Age Coefficients −3.011520.12569Standard Error 1.188020.02206 t Stat −2.534915.69706 P-value 0.020740.00002 Lower 95%−5.507460.07934 Upper 95% −0.51560.1720 a. Use the regression equation 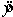 = -3.0115 + 0.1257x to determine the predicted values of y.
= -3.0115 + 0.1257x to determine the predicted values of y.
b. Use the predicted values and the actual values of y to calculate the residuals.
c. Plot the residuals against the predicted values 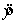 .
.
d. Does it appear that heteroscedasticity is a problem? Explain.
e. Draw a histogram of the residuals.
f. Does it appear that the errors are normally distributed? Explain.
g. Use the residuals to compute the standardised residuals.
h. Identify possible outliers.
ENS
The Enteric Nervous System (ENS) is a network of neurons lining the gastrointestinal tract, controlling digestion and gut function independently of the central nervous system.
Neuron Types
are various kinds of nerve cells classified based on their function, structure, neurotransmitter released, and direction of signal sent; including sensory, motor, and interneurons.
Neural Circuits
Complex networks of neurons that work together to carry out specific functions in the nervous system.
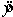 = -3.0115 + 0.1257x to determine the predicted values of y.
= -3.0115 + 0.1257x to determine the predicted values of y.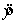 .
.