SCENARIO 12-11
a Computer Software Developer Would Like to Use

question 84

Short Answer

SCENARIO 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\ \text { R Square } & 0.7554 \\ \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\\hline\end{array}$

ANOVA
$\begin{array}{llll} \hline & {\text { df }} & {\text { SS }} &{\text { MS }} & F & \text { Significance F } \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \text { Residual } & 28 & 55386.4309 & 1978.1582 & & \\ \text { Total } & 29 & 226451.3503 & & &\end{array}$

$\begin{array}{lllll}\hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$
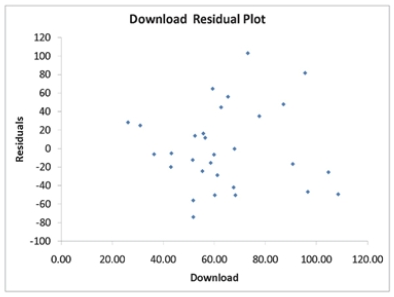Simple Linear Regression 12-41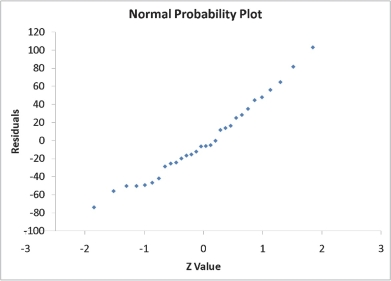
-Referring to Scenario 12-11, which of the following is the correct null hypothesis for testing whether there is a linear relationship between revenue and the number of downloads? a) $H _ { 0 } : b _ { 1 } = 0$
b) $H _ { 0 } : b _ { 1 } \neq 0$
c) $H _ { 0 } : \beta _ { 1 } = 0$
d) $H _ { 0 } : \beta _ { 1 } \neq 0$

---

Definitions:

Incremental Costs

Costs that change depending on the level of production or an alternative course of action.

Additional Revenues

Extra income generated from sources outside of the company's main business operations.

Sunk Cost

Costs that have already been incurred and cannot be recovered or reversed.

Incremental Overhead Costs

Additional overhead expenses directly resulting from a specific business decision or activity.